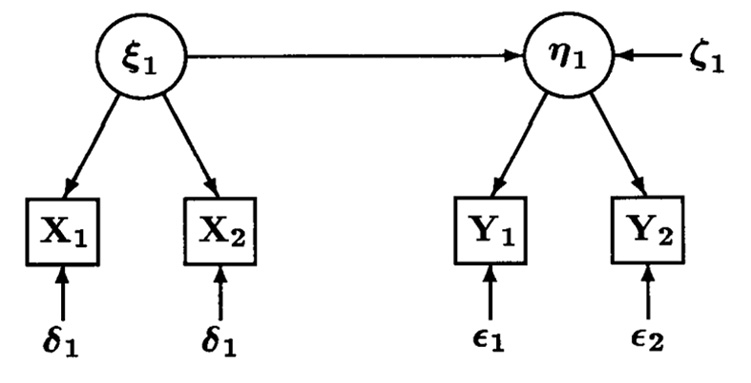
Figuur 1. Een eenvoudige LISREL-model.


Actueel Huiswerk
Data
Files voor Covariantiestructuuranalyse
Gerelateerde
Internetsites
Back to
Homepage of Anne Boomsma
Announcement
This course is
part of the
Research Master program Human Behaviour in Social Contexts.
As courses then have to be taught in English, if necessary,
and there need to be an option to study course material from books written in English, as an alternative to our own Dutch manuscript
Covariantiestructuuranalyse. If there is enough interest
the course will be lectured using Brown (2006) as a reference text.
If there are less than four students, they will be encouraged to study parts from either Boomsma (2008) or Brown (2006), under our guidence of course. For advanced students Bollen (1989) is an option to be discussed for individual study.
This course will be given in semester 1a of the academic year
2008–2009. The course fits for both master and research master students.
Inhoud en werkwijze
In dit college wordt een
inleiding gegeven in de analyse van covariantiestructuren (CSA).
Daarbij gaat het ruwweg om het volgende. Om onderlinge relaties
tussen meerdere variabelen te beschrijven kunnen inhoudelijk
gefundeerde modellen worden gemaakt, die vaak in de vorm van
schema's met `paden' worden weergegeven. De doelstelling van
onderzoekers daarbij is om vanuit theoretische overwegingen een
onderliggende structuur van gerichte relaties tussen variabelen
– vaak latente variabelen of hypothetische constructen – te
formuleren. Daarna wordt aan de hand van een steekproef van
covarianties tussen geobserveerde variabelen nagegaan in welke
mate het gepostuleerde model bij die steekproefgegevens past.
Het geheel van relaties tussen de variabelen in zo'n model, ook
wel covariantiestructuur genoemd, kan worden opgevat als een
complex `regressie-analytisch model' waarin zowel de respons-
als de verklarende variabelen aan meetfouten onderhevig kunnen
zijn. De laatste jaren wordt dit soort modellen door
sociaal-wetenschappelijke onderzoekers in toenemende mate
gehanteerd. Het programma LISREL (LIneaire Structurele
RELaties), samen met de preprocessor PRELIS, ondersteunt dit
soort analyses.
In Figuur 1 staat een eenvoudig LISREL-model met
een gerichte relatie tussen twee latente variabelen die elk door
twee geobserveerde variabelen worden gemeten. Het paddiagram
laat zien dat het model rekening houdt met mogeljke meetfouten
in de geobserveerde variabelen.

De cursus geeft een inleiding in de theoretische
achtergronden van deze vorm van statistische analyse. Praktische
oefeningen hebben tot doel het leren maken van modellen voor
covariantiestructuren en het leren werken met het LISREL- en het
PRELIS-programma. Kortom, de nadruk ligt in het college op
theoretische inzichten en praktische richtlijnen voor
onderzoekers die LISREL of een ander programma voor de analyse
van structurele modellen willen gebruiken.
Literatuur
De literatuur die in de cursus wordt besproken beslaat de
hoofdzaken uit een viertal handboeken, een persoonlijk manuscript, en een leerboek, te
weten:
De handboeken van Jöreskog et al. hoeven niet noodzakelijkerwijs
te worden aangeschaft. Het college wordt vooral gegeven aan de
hand van het manuscript van Boomsma (2006), dat verkrijgbaar is
bij de Klapperwinkel. De hoofdzaken daaruit worden in zeven
weken behandeld. Een gedetailleerd overzicht
van de inhoud wordt verderop gegeven.
Toetsing
De toetsing van de cursus valt uiteen in twee delen:
Vragen en opmerkingen
Voor vragen en opmerkingen kan contact worden opgenomen met de
docent A. Boomsma, Grote Rozenstraat 15, kamer 221, telefoon
(363)6187, e-mail a.boomsma@ppsw.rug.nl
Programmatuur
| Periode | Stof | Opgaven |
|---|---|---|
| Week 45 (02/11) | Hoofdstuk 1 | |
| Week 45 (05/11) | Hoofdstuk 2 | Ex. 1, 2 |
| Week 46 (09/11) | Hoofdstuk 4 tot 4.3 | Ex. 3, 4a |
| Week 46 (12/11) | Rest hoofdstuk 4 | Ex. 4c |
| Week 47 (16/11) | Hoofdstuk 5 | Ex. 4b |
| Week 47 (19/11) | Hoofdstuk 6 | Ex 11 |
| Week 48 (23/11) | Hoofdstuk 7 | Ex. 14b |
| Week 49 (30/11) | Hoofdstuk 8 | Ex. 5 |
| Week 49 (03/12) | Hoofdstuk 9 | Ex. – |
| Week 50 (07/12) | Hoofdstuk 12 | Ex. 12 |
| Week 51 (13/12) | Hoofdstuk 13 | Ex. 20, 23 |
| Week 51 (17/12) | Hoofdstuk 15 |
Inhoud Covariantiestructuuranalyse
Wat volgt is een overzicht van de inhoud van een boekmanuscript
over de analyse van covariantiestructuren. Het manuscript wordt
onder meer gebruikt bij de cursus M-332.
Hoofdstuk 1. Inleiding in de analyse van
covariantiestructuren
1.1 Gerichte samenhang tussen verschijnselen
1.2 Het structurele model
1.3 Het meetmodel
1.4 LISREL: een structureel model met meetfouten
1.5 Belangrijke onderzoeksvragen
1.6 Programmatuur en toepassingen
Referenties
Bijlage A. Literatuur
Hoofdstuk 2. Enige waarschijnlijkheidsrekening
2.1 Inleiding
2.2 Verdelingsaspecten van stochastische variabelen
2.3 De kansverdeling van een stochastische variabele
2.4 Stochastische onafhankelijkheid
2.5 Verwachtingswaarde
2.6 Momenten
2.7 Spreiding
2.8 Samenhang
Referenties
Hoofdstuk 3. Lineaire regressie-analyse
3.1 Het lineaire regressiemodel
3.2 De methode van de kleinste kwadraten
3.3 De geschatte regressiefunctie
3.4 Residuen
3.5 De steekproevenverdeling van b1
3.6 Inferentiële statistiek rond b1
3.7 De ANOVA-aanpak van regressie-analyse
3.8 Het multipele regressiemodel
3.9 De multipele correlatiecoëfficiënt
3.10 Regressiediagnostiek
3.11 Latente variabelen en meetfouten
Referenties
Hoofdstuk 4. Het LISREL-model
4.1 Het LISREL-model en zijn assumpties
4.2 Soorten parameters
4.3 De meeteenheid van latente variabelen
4.3.1 Illustratie van het schaalprobleem
4.3.2 Oplossingen van het schaalprobleem
4.3.3 Relatie met het identificatieprobleem
4.3.4 Gestandaardiseerde oplossingen
4.3.5 Waarschuwingen bij het schaalprobleem
Referenties
Bijlage B. Het Griekse alfabet en notaties
Hoofdstuk 5. Het identificatieprobleem
5.1 Kan het model uniek worden geschat?
5.2 Identificatievoorwaarden
5.3 Algebraïsch identificatie-onderzoek
5.4 LISREL en het identificatieprobleem
5.5 Empirische identificatie
5.5.1 Een factormodel
5.5.2 Identificatie van het model
5.5.3 Parameterschattingen
5.5.4 Empirische problemen
Referenties
Hoofdstuk 6. Klassieke schattingsmethoden
6.1 Het LISREL-model
6.2 Het schatten van het model
6.3 Schattingsmethoden
6.4 IV- en TSLS-schatters
6.5 Doelfuncties voor ULS, GLS en ML
6.6 ULS-schatters
6.7 GLS-schatters
6.8 ML-schatters
6.8.1 De aannemelijkheidsfunctie
6.8.2 De doelfunctie
6.8.3 Eigenschappen van ML-schatters
6.9 ULS-, GLS- en ML-schatters en normaliteit
6.10 Niet-normaliteit
Referenties
Hoofdstuk 7. Verdelingsvrije schattingsmethoden
7.1 Een algemene doelfunctie
7.2 Eigenschappen van schatters
7.3 De klassieke theorie: GLS en ML
7.4 De niet-klassieke theorie: WLS of ADF
7.5 Praktische problemen met WLS
7.6 DWLS-schatters
7.7 Andere schattingsmethoden
7.8 Analyse van correlatiestructuren
Referenties
Hoofdstuk 8. De passing van het model
8.1 Drie statistische onderzoeksvragen
8.2 Past het model?
8.3 Het onderzoeken van de oplossing van de analyse
8.4 Algemene, globale passingsmaten
8.5 Gedetailleerde informatie over modelpassing
8.6 Aanbevelingen bij modelmodificatie
8.7 Nieuwe chi-kwadraat-maten in LISREL
8.8 Toetsingsgrootheden van Yuan en Bentler
Referenties
Hoofdstuk 9. Modelselectie: een overzicht van maten en
indexen
9.1 Inleiding
9.2 Het probleem van modelselectie
9.3 Is het gepostuleerde model geldig? Een toets voor exacte passing
9.4 De rol en de plaats van het ware populatiemodel
9.5 Soorten fouten en discrepanties
9.6 De niet-centraliteitsparameter en de benaderingsfout
9.7 De RMSEA als functie van de benaderingsfout
9.8 Een toets voor nabije passing
9.9 Kruisvalidatie en de ECVI als schatting van de totale fout
9.10 Informatiecriteria
9.11 Globale passingsindexen
9.12 Indexen voor modelvergelijking: incrementele passingsmaten
9.13 Hoe te kiezen?
9.14 Een empirisch voorbeeld
Referenties
Hoofdstuk 10. Hypothesetoetsing en
onderscheidingsvermogen
10.1 Het toetsen van modelhypothesen
10.2 Robuustheidsonderzoek
10.3 Het toetsen van specifieke nulhypothesen
10.4 Onderscheidingsvermogen
10.4.1 Theoretische inleiding
10.4.2 Berekening van het onderscheidingsvermogen
10.4.3 Een concreet voorbeeld
10.5 Beslissingsstrategieën bij modeltoetsen
Referenties
Bijlage C. Onderscheidingsvermogen bij een factormodel
Hoofdstuk 11. Effecten en modelmodificatie
11.1 Effecten
11.2 Effecten in een schoolloopbaanmodel
11.3 Berekening van effectgrootte: nog een voorbeeld
11.4 Een voorbeeld van modelmodificatie
11.5 Een lokaal minimum
11.6 Wanneer stoppen met modificeren?
11.7 Modelspecificaties en analysestrategieën
Referenties
Bijlage D. Een basismodel voor de schoolloopbaan
Hoofdstuk 12. Schaalinvariantie en de analyse van
correlatiematrices
12.1 Schaalinvariantie en schaalvrijheid
12.1.1 Schaalinvariantie van een model
12.1.2 Schaalinvariantie van een doelfunctie
12.1.3 Schaalvrijheid van parameters
12.2 Vier mogelijke schaalkeuzen
12.3 De analyse van correlatiematrices
12.4 Samenvatting en stellingnames
Referenties
Bijlage E. Een hypothetisch model
Hoofdstuk 13. Analyse van ordinale en niet-normale
continue variabelen
13.1 Het normale verleden
13.2 Kenmerken van empirische variabelen
13.3 Twee gevallen van niet-normaliteit
13.4 Soorten variabelen
13.5 Soorten correlatiecoëfficiënten
13.6 De geanalyseerde correlatiematrix
13.7 Een Monte Carlo-onderzoek
13.8 De analyse van ordinale met andere variabelen
13.9 Samenvatting en conclusies
Referenties
Hoofdstuk 14. Iteratieve optimaliseringsprocedures
14.1 Een algemeen iteratief algoritme voor optimaliseringsproblemen
14.2 Convergentie- en stopcriteria
14.3 Het schattingsalgoritme van LISREL
Referenties
Hoofdstuk 15. De rapportage van empirische studies
Proloog
15.1 De introductie van het probleem
15.2 De theorie
15.3 De verzameling potentiële modellen
15.4 Het structurele en het meetgedeelte van het model
15.5 De populatie en de steekproef
15.6 Kenmerken van de observaties
15.7 De te analyseren momentenmatrix
15.8 De schattingsprocedure
15.9 De modelschattingen
15.10 Evaluatie en modificatie van modellen
15.11 Discussie
Referenties
Register
Goto top
Back to Homepage of Anne Boomsma
Internet Sites for Structural Equation Modeling
Institute of Aging, Portland State University, Oregon
Department of Psychology, Boston University
UGregory R. Hancock, University of Maryland
Cambridge: Cambridge University Press.
University of Los Angeles, California
J. Mack Robinson College of Business, Georgia State University,
Atlanta
J. Mack Robinson College of Business, Georgia State University,
Atlanta
Graduate School of Management, University of California, Irvine CA
Department of Psychology, University of Connecticut
Department of Psychology, University of Connecticut
Ohio State University, Columbus
Department of Psychology, Arizona State University
StatSoft (SEPATH in Statistica)
On autoregressive and simplex modeling, latent curve analysis,
and growth models
Michael Friendly, York University
John S. Uebersax, Overland Park, KS
Kano, Y., & Harada, A. (2000). Stepwise variable selection in
factor analysis. Psychometrika, 65, 7–22.
Y. Kano and A. Harada, University of Osaka, Japan
Two SAS programs as described in the paper by MacCallum, R.C.,
Browne, M.W., & Sugawara, H.M. (1996). Power analysis and
determination of sample size for covariance structure modeling.
Psychological Methods, 1, 130–149.
Richard Scheines et al., Philosophy Department, Carnegie Mellon
University, Pittsburgh
Richard Scheines et al., Philosophy Department, Carnegie Mellon
University, Pittsburgh
Notes on various topics in structural equation
modeling by Karl G. Jöreskog
Westfälische Wilhelms-Universität, Münster,
Germany
University of Austin, Texas
University of California, Los Angeles
Muthén & Muthén, University of California, Los
Angeles
E-mail: semnet@ualvm.ua.edu
Goto top
Back to Homepage of Anne Boomsma
Update: January 22, 2008